Noțiuni introductive Theoretical notions
Recursivitatea reprezintă o noţiune fundamentală a informaticii şi face parte din domeniul general al algoritmilor şi structurilor de date. Constituie o tehnică de programare care permite o exprimare extrem de concisă şi clară a algoritmilor de rezolvare a unor probleme complexe. Recursivitatea din programare este derivată în mod natural (din necesităţi practice) din noţiunea matematică. Astfel, în matematică o noţiune este definită recurent (recursiv) dacă în cadrul definiţiei apare însăşi noţiunea care se defineşte. La scrierea unui algoritm recursiv este suficient să gândim ce se întâmplă la un anumit nivel, pentru că la orice nivel se întâmplă exact acelaşi lucru. Recursion is a fundamental notion in computer science, being a part of the general domain of algorithms and data structures. It's a programming method that allows a brief and clear solution algorithm for complex problems. The notion of recursion in computer science was introduced from mathematics. In mathematics, a definition such that the object defined occurs in the definition is called a recursive definition. When writing a recursive algorithm, you just have to solve the problem for one level, because on each level happens the same thing.
Există două tipuri de recursivitate: There are two types of recursion:
- directă: dacă apelul subprogramului apare chiar în corpul său. Ex: factorial, fibonacci, fractali precum şi alte probleme din medicină – informaţia genetică conţinută în nucleul unei celule se repetă la diferite scări. direct recursion: when a function calls itself. E.g.: factorial, fibonacci, fractals and other problems from medicine, like genetic information within cell nucleus is repeted at different scales.
- indirectă: dacă apelul subprogramului recursiv apare în instrucţiunea (compusă) a unui alt subprogram care se apelează direct sau indirect din subprogramul recursiv. Ex: evaluarea unei expresii, forma poloneză prefixată a unei expresii. indirect recursion: when a function is called not by itself but by another function that it called (either directly or indirectly). E.g.: expression evaluation, polish prefix notation of an expression.
Moduri de implementare Ways of implementing
Implementare iterativă Iterative implementation
long numToPow(int number, int power) {
long result = 1;
for (int i = 0; i < power; i++) {
result *= number;
}
return result;
}
Implementare recursivă Recursive implementation
long numToPow(int number, int power) {
if (power == 0) {
return 1;
}
return number * numToPow(number, power - 1);
}
Implementare iterativă Iterative implementation
long factorial(int number) {
long result = 1;
for (int i = 1; i <= number; i++) {
result *= i;
}
return result;
}
Implementare recursivă Recursive implementation
long factorial(int number) {
if (number <= 1) {
return 1;
}
return number * factorial(number - 1);
}
Implementare iterativă Iterative implementation
long fibonacci(int number) {
long f1 = 0;
long f2 = 1;
long result = 0;
for (int i = 2; i <= number; i++) {
result = f1 + f2;
f1 = f2;
f2 = result;
}
return result;
}
Implementare recursivă Recursive implementation
long fibonacci(int number) {
if (number == 0) {
return 0;
}
if (number == 1) {
return 1;
}
return fibonacci(number - 1) + fibonacci(number - 2);
}
Reprezentare stivă Stack representation
long numToPow(int n, int p) {
if (p == 0) {
return 1;
}
return n * numToPow(n, p - 1);
}
long fact(int n) {
if (n <= 1) {
return 1;
}
return n * fact(n - 1);
}
long fibonacci(int number) {
if (number == 0) {
return 0;
}
if (number == 1) {
return 1;
}
return fibonacci(number - 1) +
fibonacci(number - 2);
}
Avantaje / Dezavantaje Advantages / Disadvantages
Datorită lucrului cu stiva la fiecare apel recursiv, un algoritm recursiv necesită un timp de lucru mai îndelungat față de același algoritm scris în mod iterativ. Due to stack opperations made at each recursive call, a recursive algorithm requires a longer execution time than the same iterative algorithm.
În cazul rulării funcției numToPow(100, 20) într-un ciclu de 10.000.000 de iterații, atât în mod iterativ, cât și recursiv, timpii obținuți au fost: The execution times of function numToPow(100, 20) in a loop of 10.000.000 steps, both iteratively and recursively, were:
Ridicarea la putere folosind funcția numToPow(n, p) Exponentiation using numToPow(n, p)
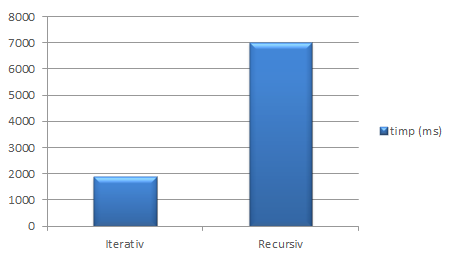
În cazul rulării funcției factorial(50) într-un ciclu de 10.000.000 de iterații, atât în mod iterativ, cât și recursiv, timpii obținuți au fost: The execution times of function factorial(50) in a loop of 10.000.000 steps, both iteratively and recursively, were:
Calcularea factorialului unui număr folosind funcția factorial(n) Computing factorial of a given number using factorial(n)
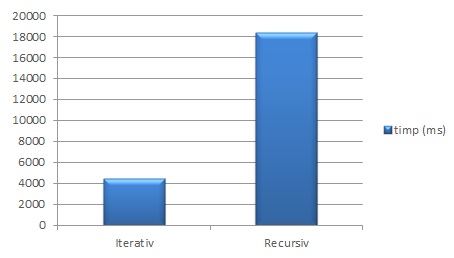
În cazul rulării funcției fibonacci(8) într-un ciclu de 10.000.000 de iterații, atât în mod iterativ, cât și recursiv, timpii obținuți au fost: The execution times of function fibonacci(8) in a loop of 10.000.000 steps, both iteratively and recursively, were:
Calcularea unei valori din secvența Fibonacci folosind funcția fibonacci(n) Computing Fibonacci value for a given number using fibonacci(n)


